Thursday, November 30, 4:00 - 5:30, Jeff 319
Pei-Lun Tseng (Queen's University)
Infinitesimal Laws of non-commutative random variables, II
In this talk, we will focus on a single type B variable,
and introduce the corresponding infinitesimal law. In
addition, we will also define the free additive
convolution for infinitesimal laws, and to see the
relation between the type B laws and the infinitesimal
laws.
Thursday, November 23, 4:00 - 5:30, Jeff 319
Pei-Lun Tseng (Queen's University)
Infinitesimal Laws of non-commutative random variables
In this talk, we will start from an infinitesimal
non-commutative probability space, and define
the freeness, and additive convolution for infinitesimal
laws. Then, we will also establish the
relation among type A free convolution, type B free
convolution, and infinitesimal free
convolution.
Tuesday, November 14, 3:30 - 5:00, Jeff 222
Pei-Lun Tseng (Queen's University)
Free independence of type B
We will continue our discussion of type B
R-transform. Then we are going to introduce the free
independence of type B, and establish the relation
between type B freeness and vanishing mixed cumulants in
type B.
Tuesday, November 7, 3:30 - 5:00, Jeff 319
Pei-Lun Tseng (Queen's University)
Non-crossing cumulants of type B
In this talk, we are going to introduce the framework of
type B non-commutative probability space. Then, we will
give the definition of the cumulants of type B and show
the relation between the cumulants of type A and the
cumulants of type B. Finally, we will discuss the
corresponding moments series and R-transform of type B.
Tuesday, October 31, 4:00 - 5:30, Jeff 319
Caleb Jonker (Queen's University)
Traffic Free Probability Spaces and Operad Independence
The discussion of non-commutative independence revolves
around what are known as universal products on
non-commutative probability spaces. These were defined
by Roland Speicher in a paper showing that there are
only three such products, yielding free independence,
tensor (classical) independence and Boolean
independence. We will expand Speicher's definition of
independence to more general types of probability spaces
focusing much of our discussion around the notion of
traffic free independence.
Thursday, October 19, 4:00 - 5:30, Jeff 319
Josué Daniel Vázquez Becerra (Queen's
University)
Liberation and the bounded cumulants property, part II
In this talk, we will show that conjugation by
certain
random unitary liberating matrices delivers the
bounded
cumulants property.
Tuesday, October 10, 4:00 - 5:30, Jeff 319
Caleb Jonker (Queen's
University)
Traffic Free Probability Spaces and Operad Independence
The discussion of non-commutative independence revolves
around what are known as universal products on
non-commutative probability spaces. These were defined
by Roland Speicher in a paper showing that there are
only three such products, yielding free independence,
tensor (classical) independence and Boolean
independence. We will expand Speicher's definition of
independence to more general types of probability spaces
focusing much of our discussion around the notion of
traffic free independence.
Tuesday, October 10, 4:00 - 5:30, Jeff 319
Josué Daniel Vázquez Becerra (Queen's University)
Liberation and the bounded cumulants property
In this talk, we will show that conjugation by certain
random unitary liberating matrices delivers the bounded
cumulants property.
Tuesday, October 3, 1:30 - 2:30, Jeff 319
Jamie Mingo (Queen's University)
The Role of the Transpose in Free Probability:
the partial transpose of R-cyclic operators, Part III
I will continue from last week.
Monday, September 25, 1:30 - 2:30, Jeff 319
Jamie Mingo (Queen's University)
The Role of the Transpose in Free Probability:
the partial transpose of R-cyclic operators, Part II
I will continue from last week.
Tuesday, September 19, 4:00 - 5:30, Jeff 319
Jamie Mingo (Queen's University)
The Role of the Transpose in Free Probability:
the partial transpose of R-cyclic operators
Like tensor independence, free independence gives us
rules for doing calculations. With random matrix models,
we usually need tensor independence of the entries and
some kind of group invariance of the joint distribution
of the entries to get the (asymptotic) freeness necessary
to apply the tools of free probability.
A few years ago Mihai Popa and I found that the transpose
also produces asymptotic freeness, i.e. a matrix could be
asymptotically free from its own transpose. Since that we
have expanded this work to the case of the partial
transposes that arise in quantum information theory.
In this talk I will explain what happens when one
transposes certain R-cyclic operators.
Previous Schedules
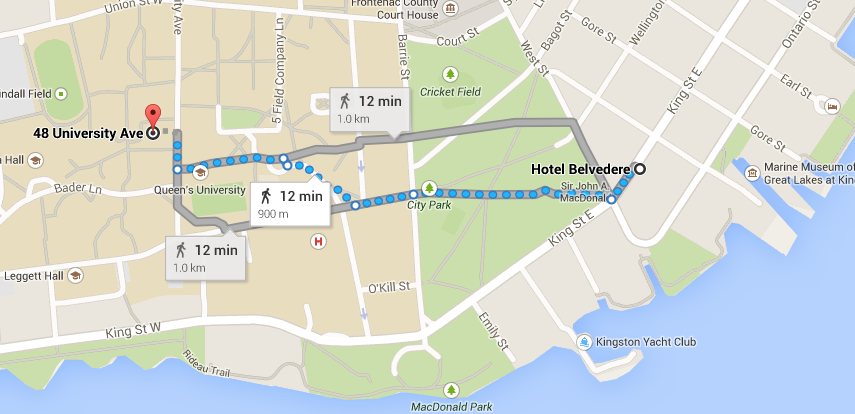
Getting to Jeffery Hall from the Hotel Belvedere