Monday, July 27, 4:30 - 6:00, Jeff 422
The Group of Symmetries and Capacity Achieving Input
Covariance Matrices of Single User Multiantenna Channels
In this talk, we will introduce the group of
symmetries of a multiantenna channel. Based on this
group and the Haar measure on it, we will derive a
theorem that generalizes many capacity theorems in the
literature. With this machinery, we will explore the
question of why the isotropic input is “good” in many
“natural” situations.
Thursday, June 25, 1:30 - 3:00, Jeff 422
Paul Skoufranis, (Texas
A & M)
On the Combinatorics of Bi-Free Probability
Free probability has been an important area of
Operator Algebras since its inception by Voiculescu.
Although originally motivated by analytic techniques,
a combinatorial approach to free probability was
developed by Speicher via the theory of non-crossing
partitions. These two approaches to free probability
each have their own advantages and many results may be
demonstrated using either approach.
Approximately two years ago, Voiculescu introduced the
notion of bi-free pairs of algebras. Voiculescu was
able to generalize many concepts in free probability
to the bi-free setting using analytic techniques. The
goal of this talk is to discuss the combinatorial
aspects of bi-free independence.
The main difference between the combinatorial
structures of free and bi-free independence come from
handling specific permutations. Consequently,
bi-non-crossing partitions must be used in place of
non-crossing partitions. Analyzing properties of
bi-non-crossing partitions yields various notions of
independences arising in bi-free probability, bi-free
partial transforms, bi-multiplicative functions for
operator-valued bi-free probability, and bi-matrix
models.
Wednesday, April 29, 4:30 - 6:00, Jeff 422
Pierre Yves Gaudreau Lamarre (uOttawa)
$*$-freeness in Families of Tensor Products of
Noncommutative Random Variables
In this talk, we will discuss the occurrence of
$*$-freeness in tensor products collections
$(a_{1;i}\otimes\cdots\otimes a_{1;K}:i\in I)$ of
noncommutative random variables with applications in
the study of asymptotic freeness for tensor products
of large random matrices. We will also investigate
connections of this work with the study of freeness in
direct products of groups.
Wednesday, April 22, 4:30 - 6:00, Jeff 422
Carlos González Guillén (uOttawa)
Euclidean distance between Haar orthogonal and
Gaussian matrices
In this talk we address the problem of how many
entries of a Haar distributed orthogonal matrix can
be jointly approximated by i.i.d. normal random
variables. In particular, we consider a gaussian
random matrix $Y(n)$ of order n and apply to it the
Gram-Schmidt orthonormalization procedure by columns
to obtain a Haar distributed orthogonal matrix
$U(n)$. If $F_i^m$ denotes the vector formed by the
first m-coordinates of the i-th row of $Y(n)-\sqrt n
U(n)$ and $m/n$ tends to $\alpha$, our main result
shows that the euclidean norm $F_i^m$ converges
exponentially fast to $f(\alpha)\sqrt m$, up to
negligible terms.
To show the extent of this result, we will see how to
use it to study the convergence of the supremum norm
$\epsilon_n(m)=\displaystyle\sup_{1\leq i \leq n, 1\leq j \leq m}
\big|\,y_{i,j}- \sqrt{n}u_{i,j}\, \big|$ and we find a coupling
that improves by a factor $\sqrt{2}$ the recently
proved best known upper bound of $\epsilon_n(m)$. We
will also discuss an application of our main result
to Quantum Information Theory.
Wednesday, April 1, 4:30 - 6:00, Jeff 422
A Lévy-Hinčin type characterization for bi-free
infinitely divisible distributions
We derive the bi-free analogue of the Lévy-Hinčin
formula for compactly supported planar probability
measures which are infinitely divisible with respect
to the additive bi-free convolution recently
introduced by Voiculescu. We also provide examples of
bi-free infinitely divisible distributions with their
bi-free Lévy-Hinčin representations, and briefly
discuss the bi-free Lévy processes. This is joint work
with H.-W. Huang and J. Mingo.
Wednesday, March 25, 4:30 - 6:00, Jeff 422
Operator-Valued Models for Multiantenna Channels and
Their Capacity: Part III
In this third and final talk we will show that the
channels introduced in the previous talk can be
studied using operator- valued free probability
theory. In particular, the capacity and capacity
achieving input covariance matrix can be efficiently
approximated using asymptotic results from random
matrix theory and free probability. We will analyze
the capacity of some concrete channels using this free
probabilistic approach. Particular emphasis will be
given to the free probabilistic modelling aspects. No
previous knowledge of free probability is
assumed. This is joint work with Victor Pérez-Abreu
(CIMAT).
Wednesday, March 18, 4:30 - 6:00, Jeff 422
Operator-Valued Models for Multiantenna Channels and
Their Capacity: Part II
Resuming from the previous time, we will start with a
theorem of Telatar in which the capacity of the so
called canonical model is computed. After that,
providing a sightly different proof, we will extend
Telatar’s theorem for a wider class of channels. To
finish the discussion on the classical work of
Telatar, we will prove rigorously an observation of
Telatar which stablished the link between asymptotic
random matrix theory and wireless communications. The
basic notions of random matrix theory will be
explained as needed.
Tuesday, March 10, 3:30 - 5:00, Jeff 222
Unitary Valued Brownian Motion
This is a report on a joint work with Todd Kemp and
Antoine Dahlqvist. Biane prove that the unitary
Brownian motion converges in distribution to the free
unitary Brownian motion. We prove that this
convergence is strong. The proof relies on
combinatorics, stochastic calculus, and an ‘unfolding
trick’. We will mention some applications of this
result, too.
Wednesday, March 4, 4:30 - 6:00, Jeff 422
Operator-Valued Models for Multiantenna Channels and
Their Capacity: Part I
About 20 years ago, multiantenna systems
appeared. Since then, random matrix theory has been
one of the main tools for the design and analysis of
these systems. With recent developments in free
probability theory, it is now possible to study these
systems using what we called operator-valued
models. In particular, we are able to study the
information theoretic capacity in a very efficient
way.
In this first talk, we will provide a terse
introduction to the communication and information
theory required to settle down the main capacity
theorems for multiantenna channels. We will emphasize
the role of certain random matrix theory results in
the aforementioned theorems. At the end, we will
discuss some random matrix theory questions arising in
this context.
Tuesday, February 11, 4:30 - 6:00, Jeff 422
Continuous Spectrum, Orbit Equivalence
We investigate the existence of a continuous
eigenvalue for a Cantor minimal system, $(X, T)$, with
regards to its dimension group, $K_0(X, T)$. In this
context, the notion of irrational mixability for
dimension groups is introduced and some (necessary
and) sufficient conditions for this property will be
given. The main property of these dimension groups is
the absence of irrational values in the set of
continuous spectrum of their realizations by Cantor
minimal systems. Any realization of an irrationally
mixable dimension group with cyclic rational subgroup
is weakly mixing and cannot be (strong) orbit
equivalent to a Cantor minimal system with non-trivial
spectrum. The talk is based on a recent joint work
with Theirry Giordano and David Handelman.
Tuesday, February 3, 4:00 - 5:30, Jeff 202
Free infinitely divisible laws and free Lévy-Hincin
formula, IV
We will discuss infinitely divisible compactly
supported probability measures relative to free
convolution on the real line by using function
theory. The content of the talk is based on the work
of Bercovici and Voiculescu.
Wednesday, January 28, 4:30 - 6:00, Jeff 422
Free infinitely divisible laws and free Lévy-Hincin
formula, III
We will discuss infinitely divisible compactly
supported probability measures relative to free
convolution on the real line by using function
theory. The content of the talk is based on the work
of Bercovici and Voiculescu.
Wednesday, January 21, 4:30 - 6:00, Jeff 422
Second Order Cumulants for Partially Transposed
Wishart Matrices, II
I will continue from last week.
Wednesday, January 14, 4:30 - 6:00, Jeff 422
Second Order Cumulants for Partially Transposed
Wishart Matrices
Wishart matrices are a basic tool in multivariate
analysis. Recently partially transposed Wishart
matrices have become an object of interest in quantum
information theory as G. Aubrun showed that a
partially transposed Wishart matrix is asymptotically
semi-circular; this means that all free cumulants
above $\kappa_2$ vanish. M. Popa and I have shown that
the full and partial transpose operation is
asymptotically liberating. In this talk I will explain
what second order cumulants are and how to compute
them for a partially transposed Wishart matrix. It
turns out that most, but not all, vanish.
Previous Schedules
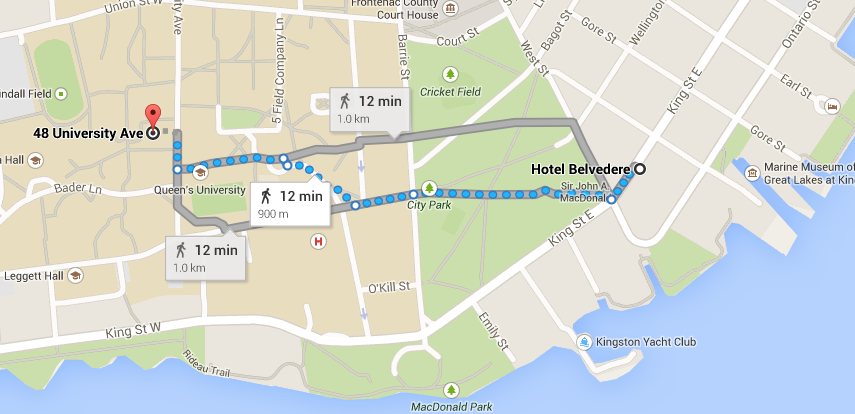
Getting to Jeffery Hall from the Hotel Belvedere